스택이란?
접시를 차곡차곡 쌓았다가 맨 위의 접시부터 다시 꺼내어 사용하는 것처럼, 추가된 데이터 원소들을 끄집어내면 마지막에 넣었던 것부터 넣는 순서의 역순으로 꺼내지는 자료구조를 스택(stack)이라고 부른다.
이처럼 마지막에 넣은 것이 가장 먼저 꺼내어지는 성질 때문에 스택을 다른말로는 후입선출(LIFO, last-in first-out) 자료 구조라고도 한다.
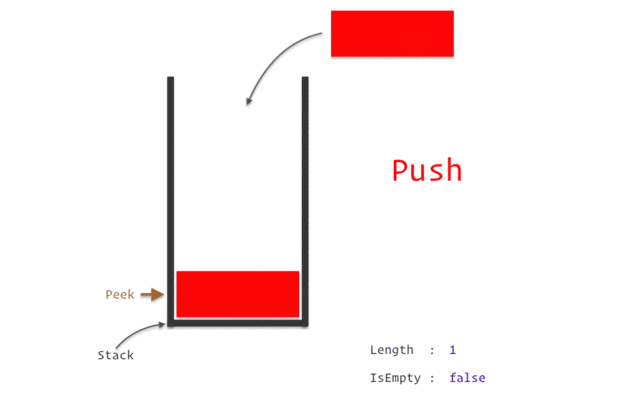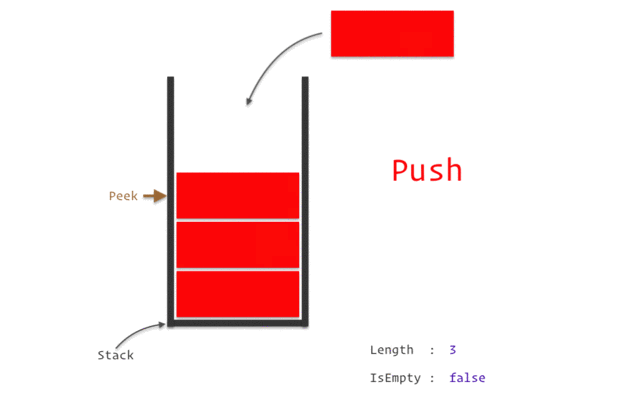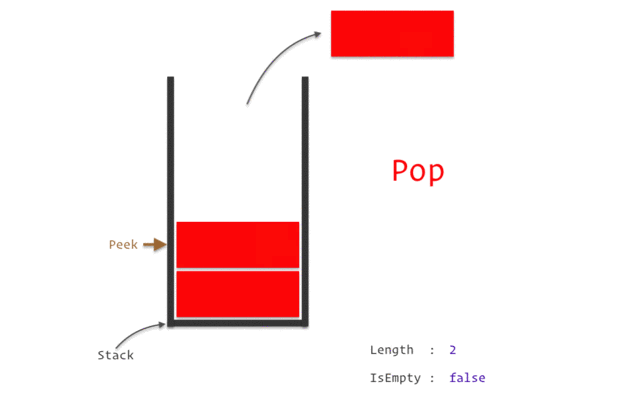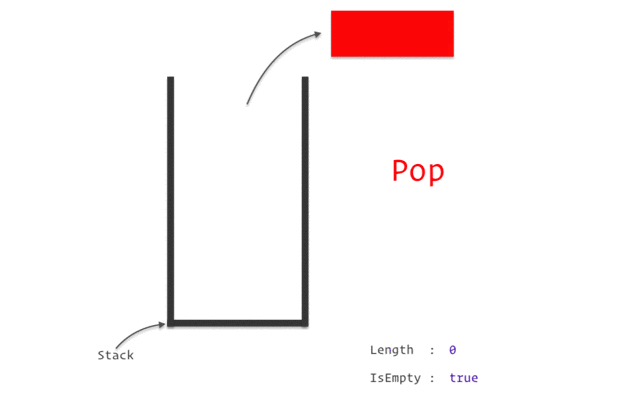
스택이 지원하는 연산 목록
- size() - 현재 스택에 들어 있는 데이터 원소의 수를 구한다.
- isEmpty() - 현재 스택이 비어있는지 판단한다.
- push(x) - 데이터 원소 x를 스택에 추가한다.
- pop() - 스택의 맨 위에 저장된 데이터 원소를 제거하면서 반환한다.
- peek() - 스택의 맨 위에 저장된 데이터 원소를 반환한다.
배열을 이용한 스택 파이썬 구현
class ArrayStack:
def __init__(self):
self.data = []
def size(self):
return len(self.data)
def isEmpty(self):
return self.size() == 0
def push(self, item):
self.data.append(item)
def pop(self):
return self.data.pop()
def peek(self):
return self.data[-1]
s = ArrayStack()
s.push(3)
print("peek : ", s.peek()) # peek : 3
s.push(5)
print("peek : ", s.peek()) # peek : 5
s.push(8)
print("peek : ", s.peek()) # peek : 8
print("size : ", s.size()) # size : 3
print("pop : ", s.pop()) # pop : 8
스택 라이브러리
# pythonds 라이브러리를 설치
from pythonds.basic.stack import Stack
S = Stack()
dir(S)
# ['__doc__', '__init__', '__module__', 'isEmpty', 'items', 'peek', 'pop', 'push', 'size']
스택의 응용 - 수식의 후위표기법(Postfix Notation)
수식의 후위 표기법과 중위표기법
일상에서 사용하는 수식의 표기법은, 중위표기법(infix notation)이라고 부른다.
두 개의 피연산자 A와 B를 가지고 덧셈을 하는 수식을 표기하면 A + B와 같이 되는데, 이 때 연산자인 + 가 두 피연산자의 사이에 위치하기 때문에 중위 표기법이라고 부른다.
후위 표기법은 연산자를 두 피연산자 뒤에 쓰는 방식이다. 따라서 앞의 예인 A + B를 후위 표기법으로 표기하면 AB+가 된다. 후위 표기법을 사용하면 괄호를 사용하지 않아도 연산의 우선순위를 수식에 표현할 수 있다.
예를 들어, 중위 표기법으로 표기된 (A + B) * (C + D)를 후위 표기법으로 변환하여 쓰면 A B + C D + * 가 된다.
알고리즘 설계
- 중위표현식을 왼쪽부터 한 글자씩 읽어서 피연산자이면 그냥 출력한다.
- '(' 이면 스택에 push하고, ')' 이면 '(' 이 나올 때까지 스택에서 pop하여 출력한다.
- 연산자이면 스택에서 이보다 높거나 같은 우선순위 것들을 pop하여 출력한다.
- 연산자를 모두 pop한 뒤에 만나는 연산자는 스택에 push한다.
- 수식에 끝까지 갔을 때, 스택에 남아 있는 연산자는 모두 pop하여 출력한다.
후위표기법 파이썬 구현
class ArrayStack:
ㆍㆍㆍ
prec = {
'*': 3, '/': 3,
'+': 2, '-': 2,
'(': 1
}
def solution(S):
opStack = ArrayStack()
answer = ''
for i in S:
# 알고리즘 설계 1.
if i.isalpha():
answer += i
# 알고리즘 설계 2.
elif i == '(':
opStack.push(i)
elif i == ')':
while not opStack.isEmpty():
op = opStack.pop()
if op == '(':
break
else:
answer += op
else:
# 알고리즘 설계 3.
if not opStack.isEmpty():
while not opStack.isEmpty():
if prec[opStack.peek()] >= prec[i]:
answer += opStack.pop()
else:
break
# 알고리즘 설계 4.
opStack.push(i)
else:
opStack.push(i)
# 알고리즘 설계 5.
while not opStack.isEmpty():
answer += opStack.pop()
return answer
print(solution("(A+B)*(C+D)")) # A B + C D + *- (A+B) * (C+D)일 때, 알고리즘 설계 2.를 만나, ( 가 stack에 push된다.
- opStack = [ '(' ]
- A는 알고리즘 설계 1.을 만나 answer에 저장된다.
- opStack = [ '(' ]
- answer = 'A'
- +는 알고리즘 설계 3.을 만나 prec[opStack.peek() = '(' 과 prec[i] = '+'을 비교하여 while문을 돌고, if 조건에 맞지 않아, brack 후 opStack.push(i)를 하게 된다.
- opStack = [ '(', '+' ]
- answer = 'A'
- B는 알고리즘 설계 1.을 만나 answer에 저장된다.
- opStack = [ '(', '+' ]
- answer = 'AB'
- ')' 를 만나 알고리즘 설계 2.를 만나 answer에 pop한 값들을 더한다.
- opStack = [ ]
- answer = 'AB+'
- '*' 는 opStack이 비어있으니, 알고리즘 설계 4.을 만나 opStack에 push된다.
- opStack = [ '*' ]
- answer = 'AB+'
- 다시 1번부터 5번을 반복한다.
- opStack = [ '*' ]
- answer = 'AB+CD+'
- 마지막 알고리즘 설계 6.을 만나서 opStack에 들어있던, '*'도 pop되어 answer에 저장된다.
- opStack = [ ]
- answer = 'AB+CD+*
후위 표기 수식 계산
알고리즘 설계
- 후위 표현식을 왼쪽부터 한 글자씩 읽어서 피연산자이면 스택에 push한다.
- 연산자를 만나면 스택에서 pop -> 변수 1, 또, pop하여 변수 2에 넣고 2와 1을 계산한 후 이 결과를 스택에 push한다.
- 위 과정을 반복하다가 수식의 끝에 도달하면 스택에서 pop하면 이것이 계산 결과이다.
후위 표기 수식 계산 파이썬 구현
class ArrayStack:
ㆍㆍㆍ
def splitTokens(exprStr):
tokens = []
val = 0
valProcessing = False
for c in exprStr:
if c == ' ':
continue
if c in '0123456789':
val = val * 10 + int(c)
valProcessing = True
else:
if valProcessing:
tokens.append(val)
val = 0
valProcessing = False
tokens.append(c)
if valProcessing:
tokens.append(val)
return tokens
def infixToPostfix(tokenList):
prec = {
'*': 3,
'/': 3,
'+': 2,
'-': 2,
'(': 1,
}
opStack = ArrayStack()
postfixList = []
for i in tokenList:
if type(i) is int:
postfixList.append(i)
elif i == '(':
opStack.push(i)
elif i == ')':
while not opStack.isEmpty():
op = opStack.pop()
if op == '(':
break
else:
postfixList.append(op)
else:
if not opStack.isEmpty():
while not opStack.isEmpty():
if prec[opStack.peek()] >= prec[i]:
postfixList.append(opStack.pop())
else:
break
opStack.push(i)
else:
opStack.push(i)
while not opStack.isEmpty():
postfixList.append(opStack.pop())
return postfixList
def postfixEval(tokenList):
valStack = ArrayStack()
for i in tokenList:
if i == '+':
first_val = valStack.pop()
second_val = valStack.pop()
valStack.push(first_val + second_val)
elif i == '-':
first_val = valStack.pop()
second_val = valStack.pop()
valStack.push(second_val - first_val)
elif i == '*':
first_val = valStack.pop()
second_val = valStack.pop()
valStack.push(first_val * second_val)
elif i == '/':
first_val = valStack.pop()
second_val = valStack.pop()
valStack.push(second_val / first_val)
else:
valStack.push(i)
result = valStack.pop()
return result
def solution(expr):
tokens = splitTokens(expr)
postfix = infixToPostfix(tokens)
val = postfixEval(postfix)
return val
a = "(1+4)*5"
b = solution(a)
print(b) # 25'CS > Data Structure' 카테고리의 다른 글
| 환형 큐(Circular Queues) (0) | 2022.09.18 |
|---|---|
| 큐 (Queues) (0) | 2022.09.11 |
| 양방향 연결 리스트(Doubly Linked Lists) (0) | 2022.08.30 |
| 연결 리스트 (Linked Lists) (0) | 2022.08.21 |
| 선형 배열(Linear Array) (0) | 2022.08.11 |
